탐욕 알고리즘(Greedy)
‘Greedy Algorithm’ 은 탐욕법이라고도 하며 현재 상황에서 당장 좋은 선택만 고르는 방법
그리디 알고리즘은 매 순간 가장 좋아 보이는 것만 선택하며 현재의 선택이 나중에 미칠 영향에 대해서는 고려하지 않는다.
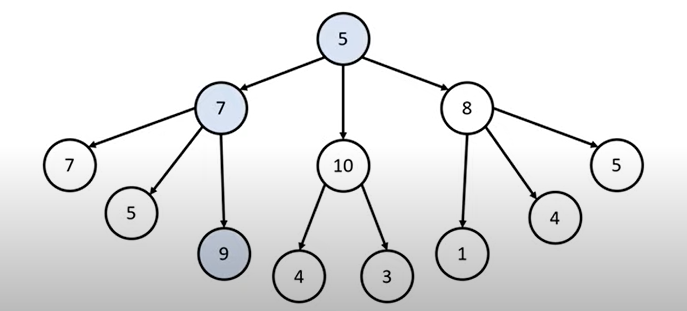
아래 루트 노드 부터 시작해서 거쳐가는 노드 의 합을 최대로 만들어야 할 때 최적해 는 무엇일까?
루트 노드(Root Node) - 노드는 매듭, 절, 집합점, 중심점이라는 사전적 의미로 최상위 집합점을 일컫는다.
최적해 - 선형 계획법에서, 제약 조건을 충족시킬 수 있는 해 가운데 목적 함숫값을 최대 또는 최소로 만드는 값이다.
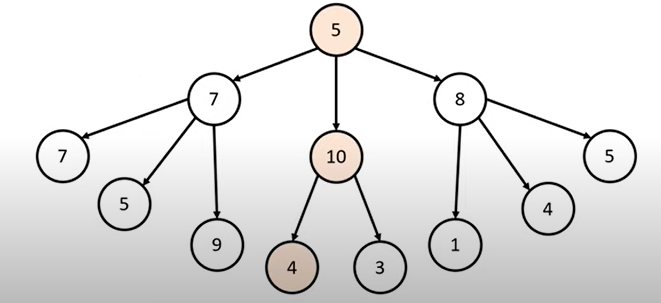
위와 같이 최적해의 경로는 5 → 7 → 9 임을 알 수 있지만 반면 그리디 알고리즘은 아래와 같이 매순간 선택지 중 가장 최적의 해만 고르게된다.
이러한 이유로 일반적인 상황에서 그리디 알고리즘은 최적의 해를 보장할 수 없을 때가 많습니다. 하지만 코딩 테스트에서의 대부분의 그리디 문제는 탐욕법으로 얻은 해가 최적의 해가 되는 상황에서, 이를 추론할 수 있어야 풀리도록 출제가 된다고 합니다.
그리디 알고리즘은 기준에 따라 좋은 것을 선택하는 알고리즘이므로 문제에서 가장 큰 순서, 가장 작은 순서와 같은 기준을 제시해 준다.
실전문제
등산가 김강산은 가족들과 함께 캠핑을 떠났다. 하지만, 캠핑장에는 다음과 같은 경고문이 쓰여 있었다. 캠핑장은 연속하는 20일 중 10일동안만 사용할 수 있습니다. 강산이는 이제 막 28일 휴가를 시작했다. 이번 휴가 기간 동안 강산이는 캠핑장을 며칠동안 사용할 수 있을까? 강산이는 조금 더 일반화해서 문제를 풀려고 한다. 캠핑장을 연속하는 P일 중, L일 동안만 사용할 수 있다. 강산이는 이제 막 V일 짜리 휴가를 시작했다. 강산이가 캠핑장을 최대 며칠동안 사용할 수 있을까? (1 < L < P < V)
입력은 여러 개의 테스트 케이스로 이루어져 있다. 각 테스트 케이스는 한 줄로 이루어져 있고, L, P, V를 순서대로 포함하고 있다. 모든 입력 정수는 int범위이다. 마지막 줄에는 0이 3개 주어진다.
이 문제에서는 캠핑장을 연속하는 P일 중, L일 동안만 사용할 수 있다. 이때 휴가가 V일일 때 캠핑장을 최대 며칠 동안 사용할 수 있는지 구하면 된다.
문제를 이해한 후 가설을 세워본다. 아래와 같이 총 28일의 휴가가 있다.
◼◼◼◼◼ ◼◼◼◼◼ ◼◼◼◼◼ ◼◼◼◼◼ ◼◼◼◼◼ ◼◼◼
연속하는 20일 중 10일만 사용 할 수 있기 때문에 10일을 꽉 채워 붙여 사용한다 가정한다. 이 부분을 공식화 하면 L * (V/P) 즉 10 * (28/20)와 같다.
◻◻◻◻◻ ◻◻◻◻◻ ⅹⅹⅹⅹⅹ ⅹⅹⅹⅹⅹ ◼◼◼◼◼ ◼◼◼
이 경우 연속하는 20일 중 10일은 사용하고 10일은 사용이 불가했다. 남은 휴가는 8일. 연속하는 20일이 지났기 때문에 다시 캠핑장을 이용할 수 있게 되어 남은 8일을 캠핑장을 이용할 수 있다.
이 부분을 공식화 하면 남은휴가 8일 = L 일경우 L*(V/P) + L 와 남은휴가 8일 != L 일경우 L*(V/P) + (V%P)의 경우로 찾을 수 있다.
◻◻◻◻◻ ◻◻◻◻◻ ⅹⅹⅹⅹⅹ ⅹⅹⅹⅹⅹ ◻◻◻◻◻ ◻◻◻
문제와 함께 제공된 몇 가지 케이스에 대해 위의 방법으로 풀이를 진행하면 패턴을 알 수 있다. 이 패턴을 공식화하면 아래와 같다.
\[total = L * (V/P) + Math.min(L, (V\%P))\]